[最も共有された！ √] 三角形の角の二等分線と比 225551-三角形の角の二等分線と比 証明

頂角の二等分線が底辺を分割するときの比に関する問題 大垣日大高校入試問題より 身勝手な主張

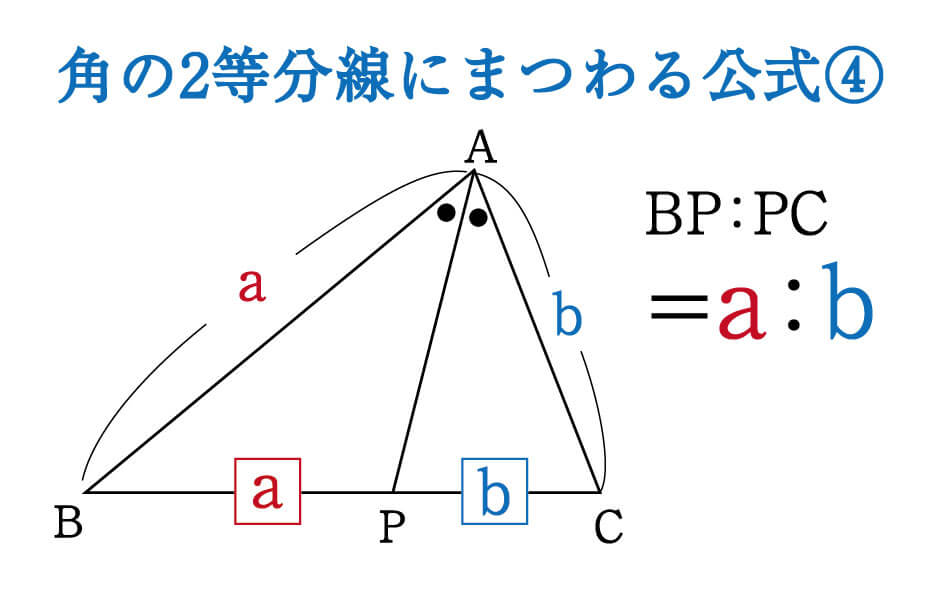
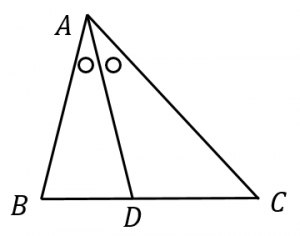
角の二等分線と補助線 角の二等分線の性質 ABC において右図2のように線分 AD が∠ A を二等分しているとき， BDDC=BAAC が成り立ちます． ※この定理は中学校では習いませんので，中学生に対して「覚えなさい」とか「この問題がよく出る」という 角の二等分線を引くと次のようになる。 AD の長さを求めるために，ADを含む三角形を探すと A B D と A C D が見つかる。 A B C の面積を求めることができることを利用して，ADの長さを求めよう。 A B C = A B D A C D 1 2 AB ∙ AC sin ⁡ 1 ° = 1 2 AB ∙ AD sin ⁡ 60 ° 1

三角形の角の二等分線と比 証明

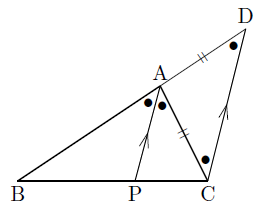
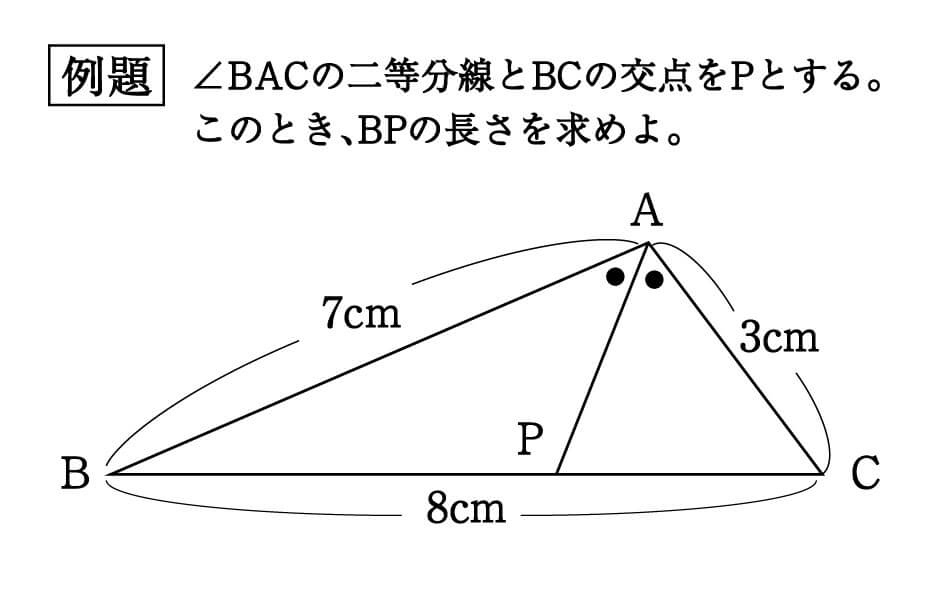
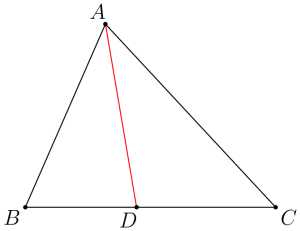
三角形の角の二等分線と比 証明-∠bacの二等分線と辺bcの交点をdとする。次の問いに答えよ。 ab=4,ac=10,bc=7のとき bdを求めよ。 a b c d ac=9,bd=3,dc=4 のときabを三角形の角の二等分線と辺の比の証明 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 このテキストでは、この定理を証明します。 次に、下図のように頂点Cを通り 直線ADと平行な直線 をひく。 の二等辺三角形

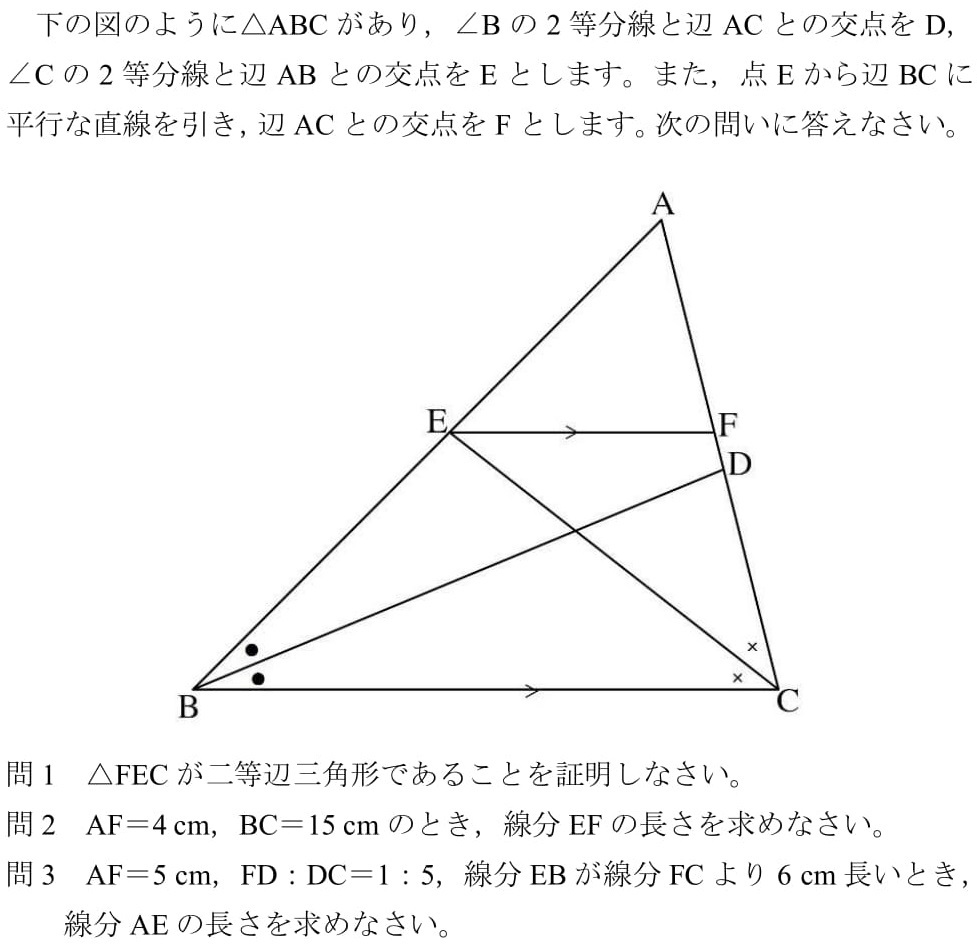
角の2等分線超難問 いつかの大分県 高校入試 数学 良問 難問

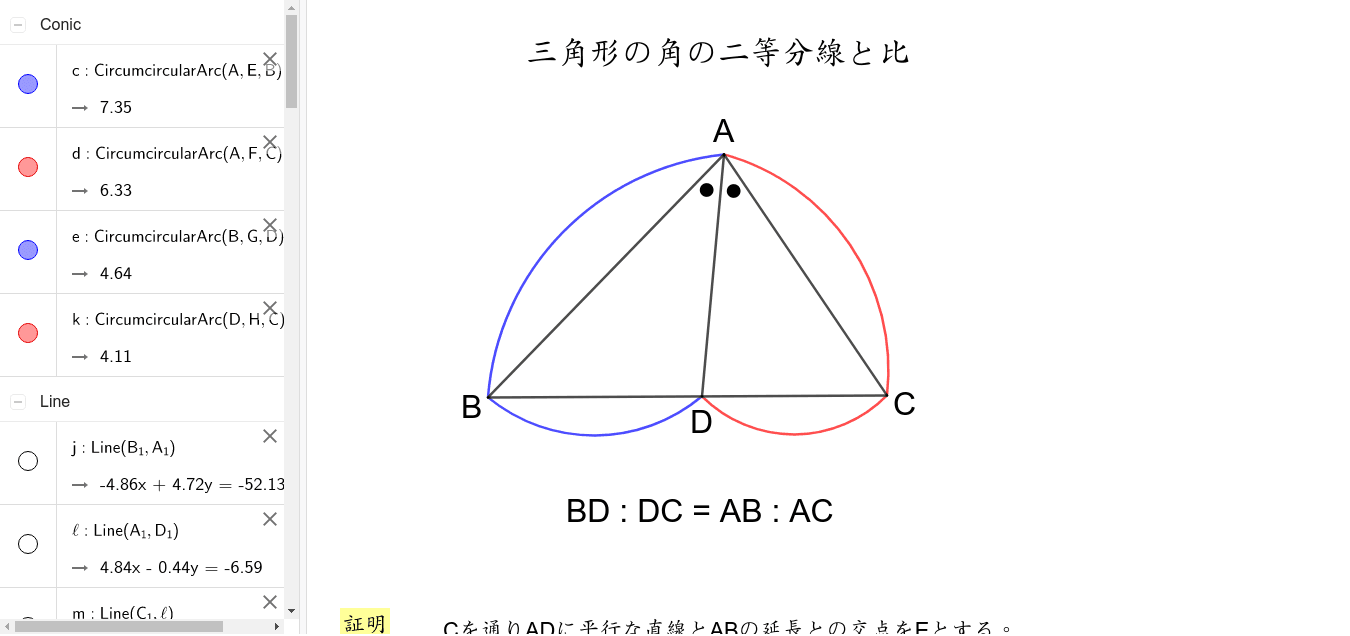
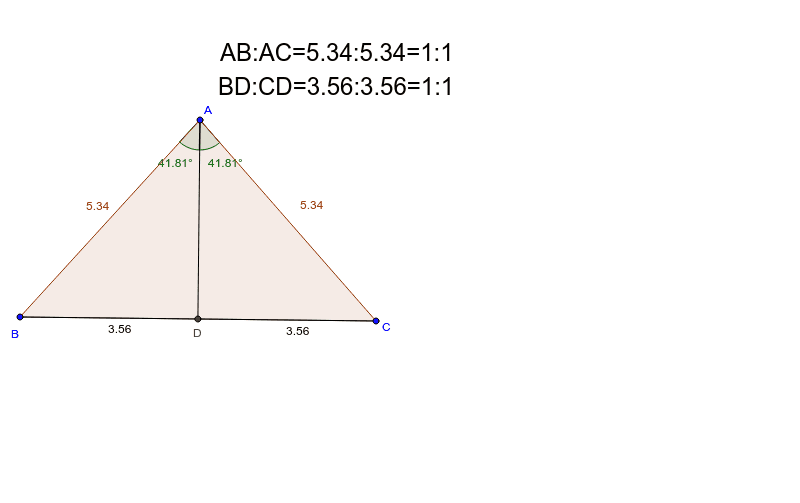
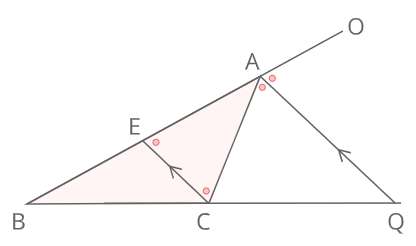
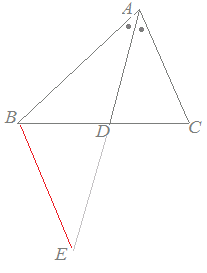
 定理1 ABC A B C の ∠A ∠ A の2等分線と辺 BC B C との交点を D D とすると, AB AC = BD DC A B A C = B D D C が成り立つ また, 三角形の外角の二等分線に関しても同様の定理が成り立ちます 定理2 AB ≠ AC A B ≠ A C である ABC A B C の ∠A ∠ A の外角の2等分線と辺 BC B C 三角形の角の二等分線による対辺の分割 三角形の任意の角の二等分線を引くと、対辺を残りの2辺の比に分割する。 図を交えて記述すると、次のようになります。 証明は以下の通りです。 頂点Cを通り、ADに平行な直線を引き、ABとの交点をEとします角度を単位円上の点として扱う幾何代数の技法によって、角の二等分線の性質を確認します。 クリフォード代数は使用しないで、複素平面上でオイラーの公式に基づく計算を行います。 ※ 図は Markdown に SVG を直接記述しています

 外角の公式では、内角の公式と 項の順序が逆になっている ことに注意しましょう。 性質②二等分線と辺の比 さらに、角の二等分線によって分けられた辺とそれ以外の辺との間に、以下の性質が成り立ちます。 \}{頂角が60°,\ 90°,\ 1°\ の場合$ { } ${二等分線の長さをxとおき,\ 面積を2通りに表す$ ${3辺の長さが判明している場合$ { } ${角の二等分線と辺の比の関係\ {ABAC=BDDC}\ (数\text A)\ を用いる$ に余弦定理を適用し,\ {3辺の長さからcos Bを求める$ に余弦定理を適用 内角の二等分線の定理から辺の長さの比になる。したがって二等辺三角形のときだけ、面積を二等分する。 内角の二等分線の定理 三角形abcで角aの二等分線とbcの交点をdとすると、abac=bddc ナイス！ 横浜関内でグラサンだった老人

三角形の角の二等分線と比 証明のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	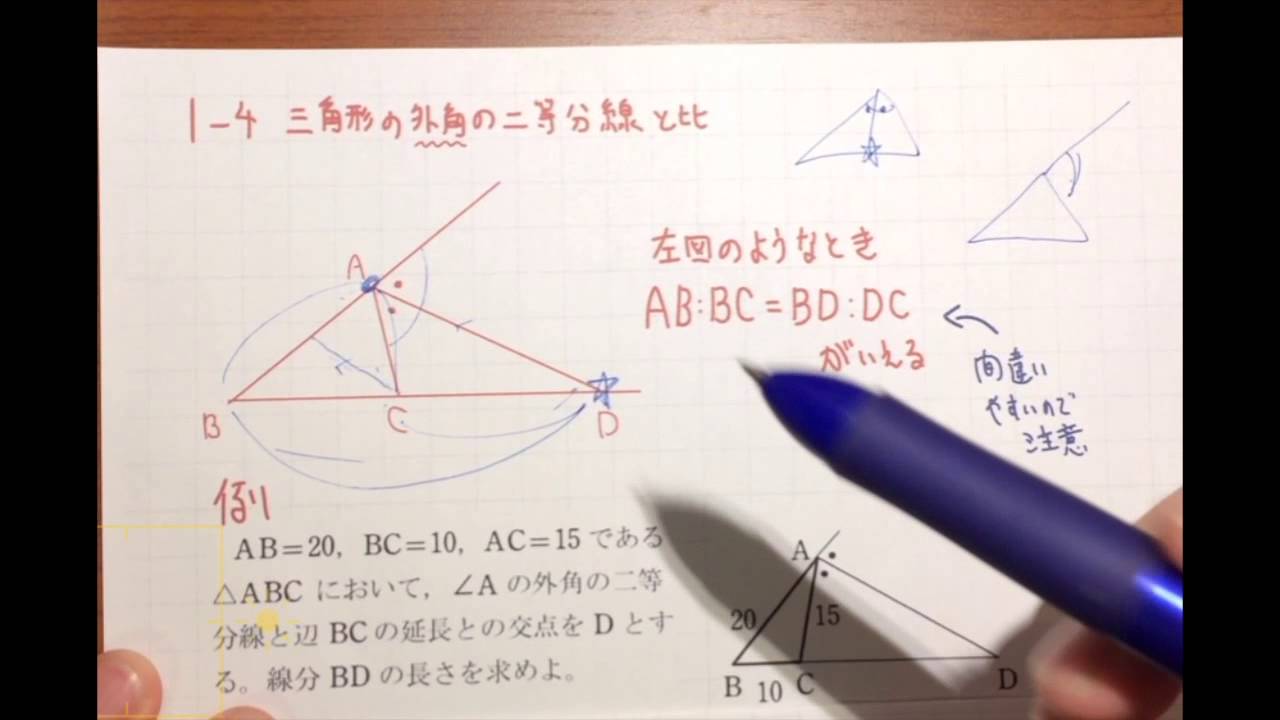二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	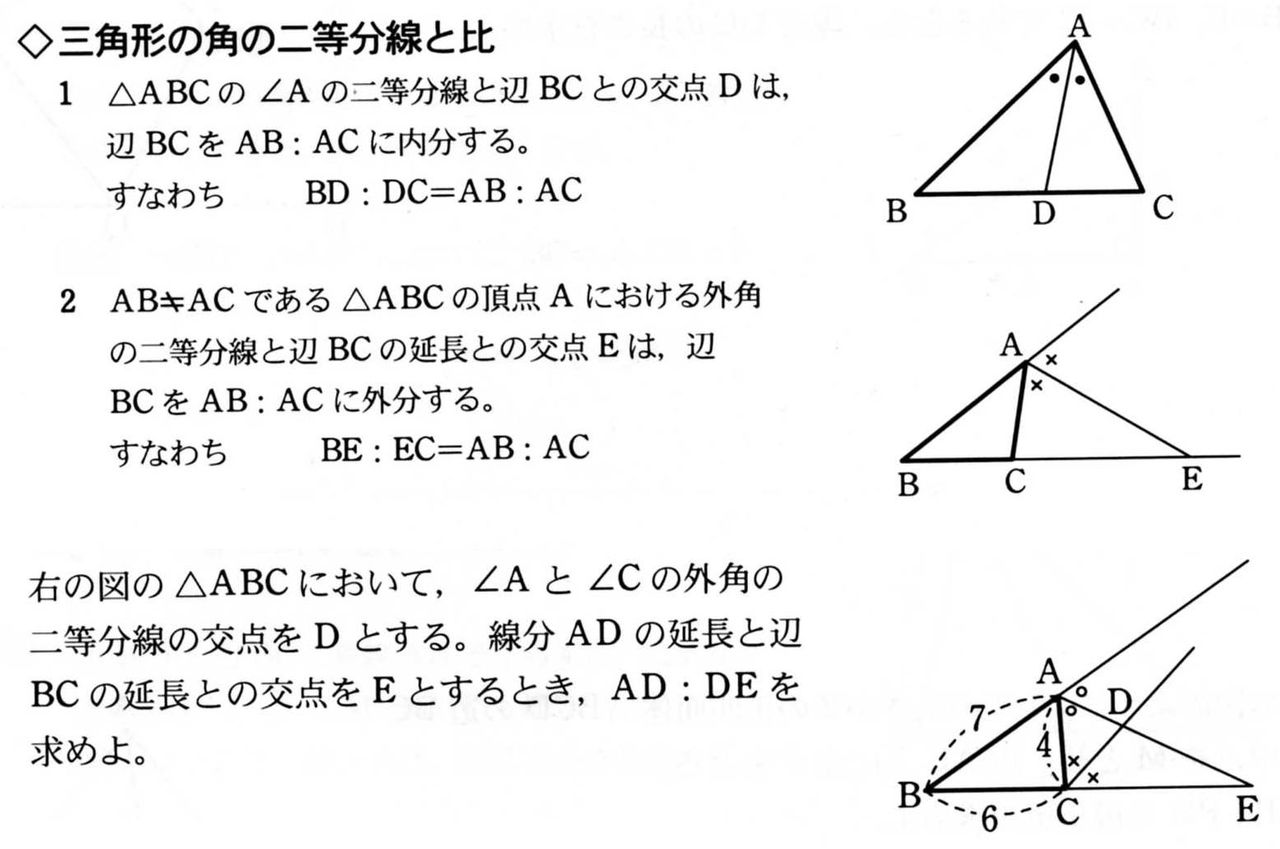二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	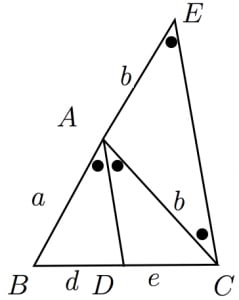二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	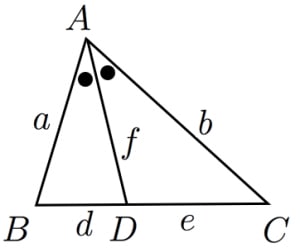二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	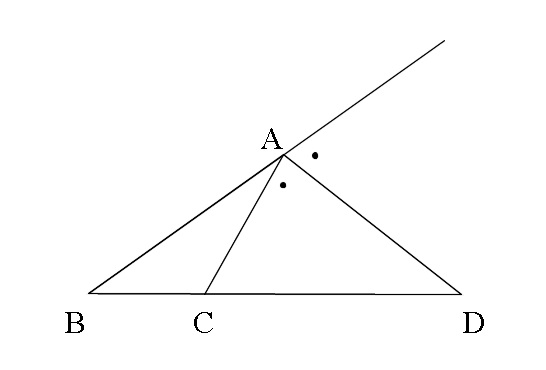二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	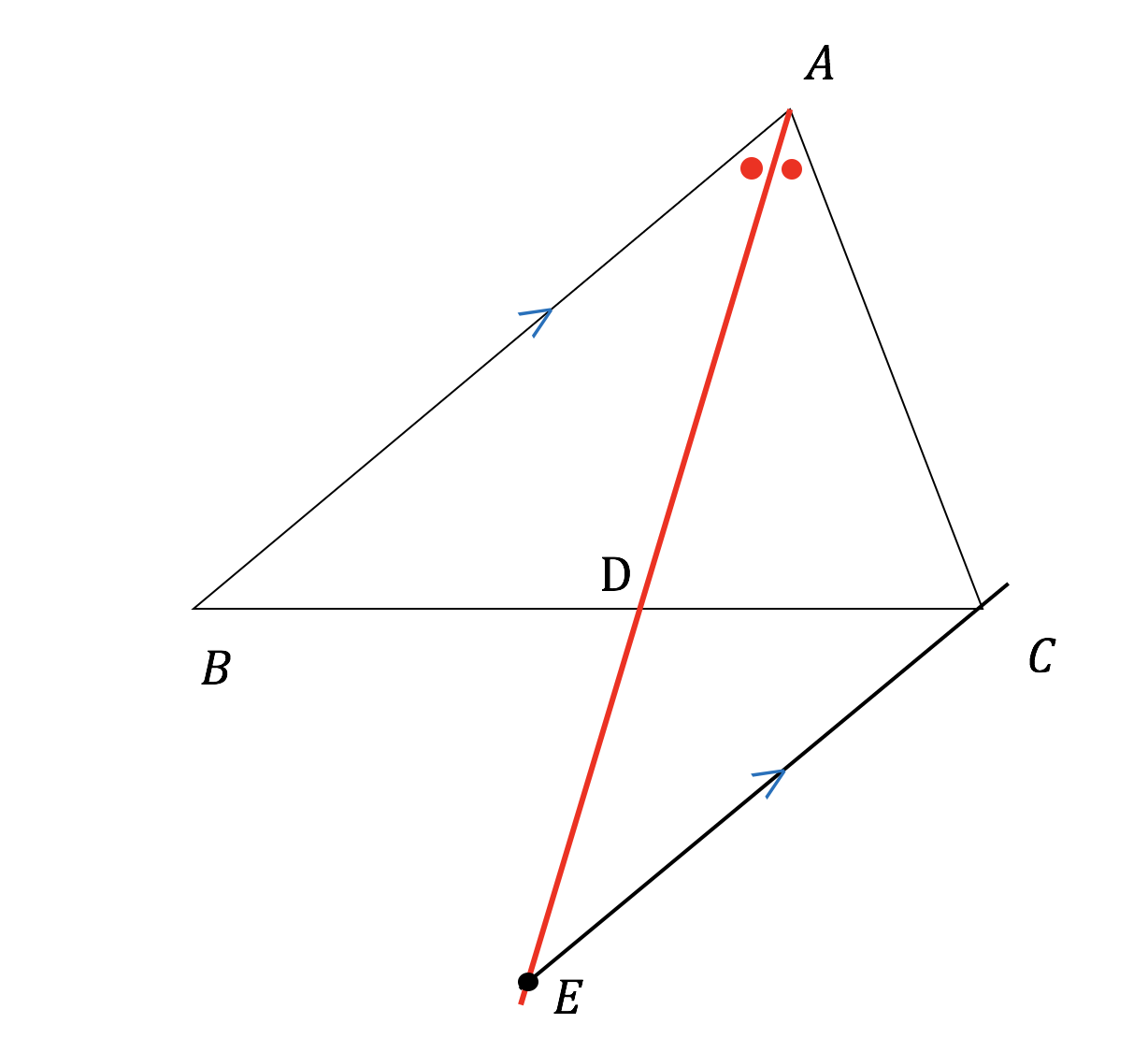二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	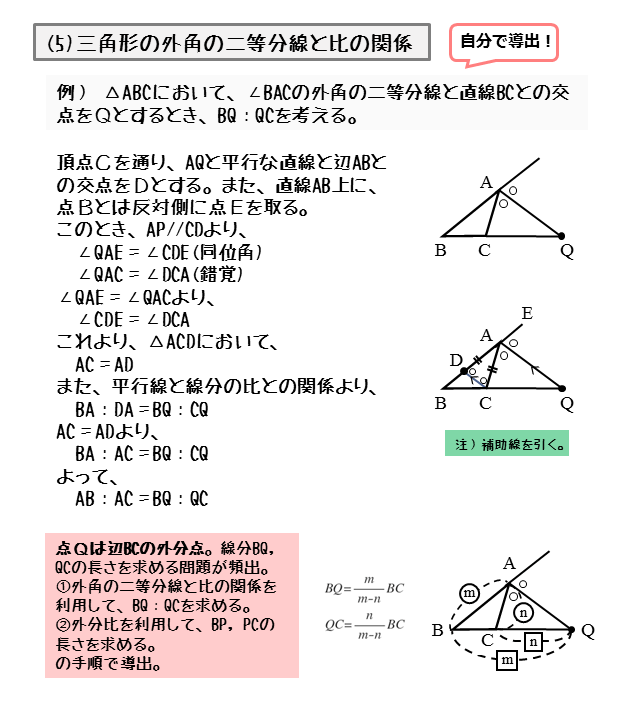二等分線と垂線の定理 Fukusukeの数学めも	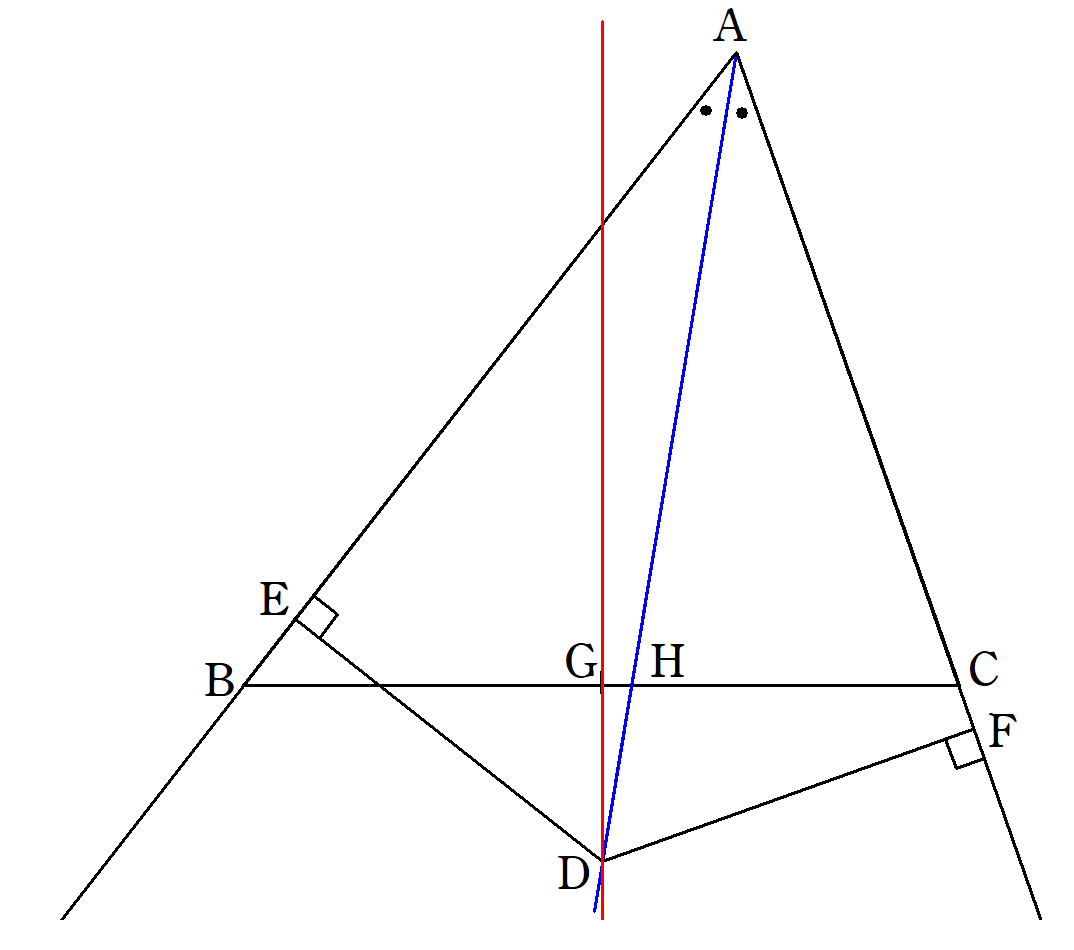二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	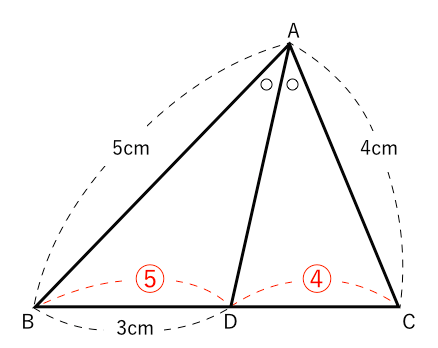二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも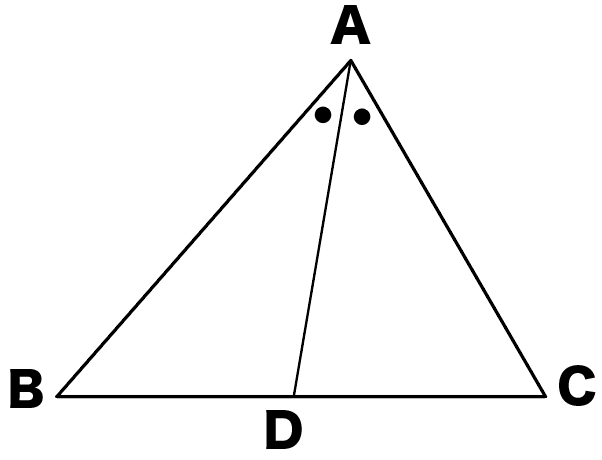
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	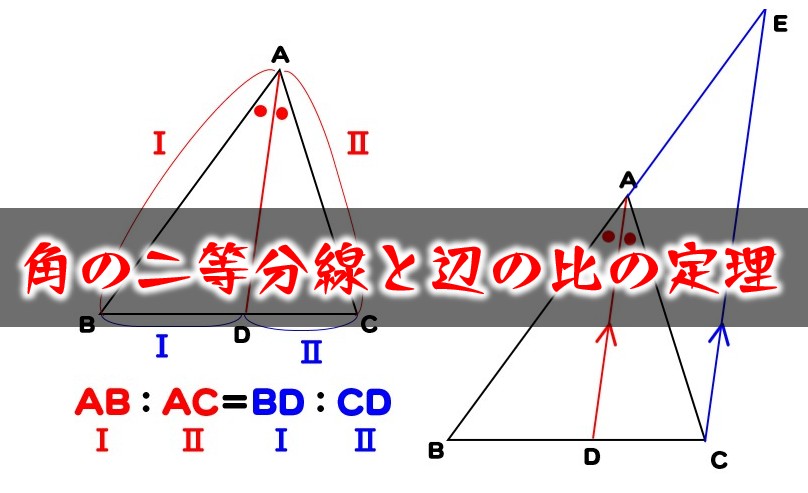二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも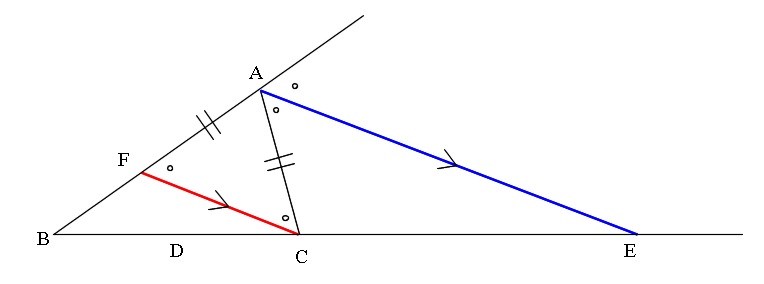
二等分線と垂線の定理 Fukusukeの数学めも	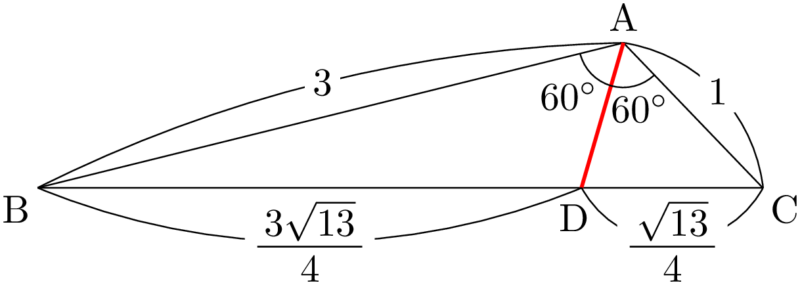二等分線と垂線の定理 Fukusukeの数学めも	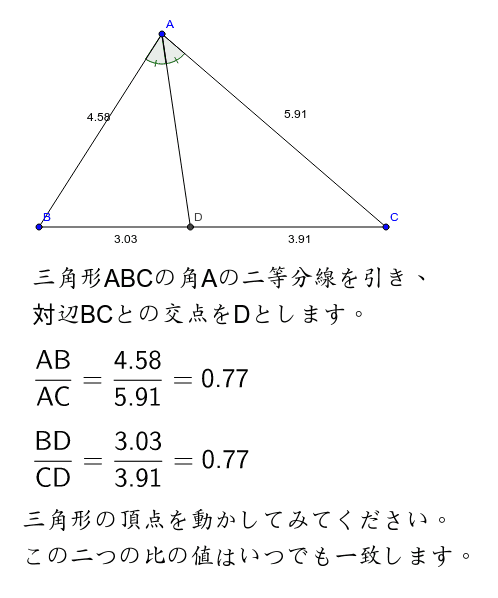二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも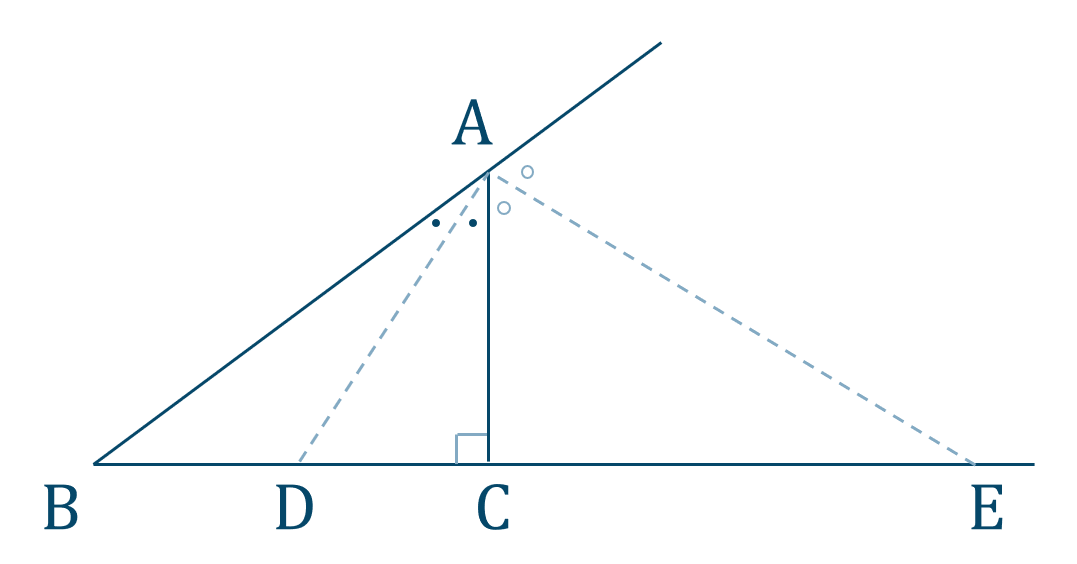
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも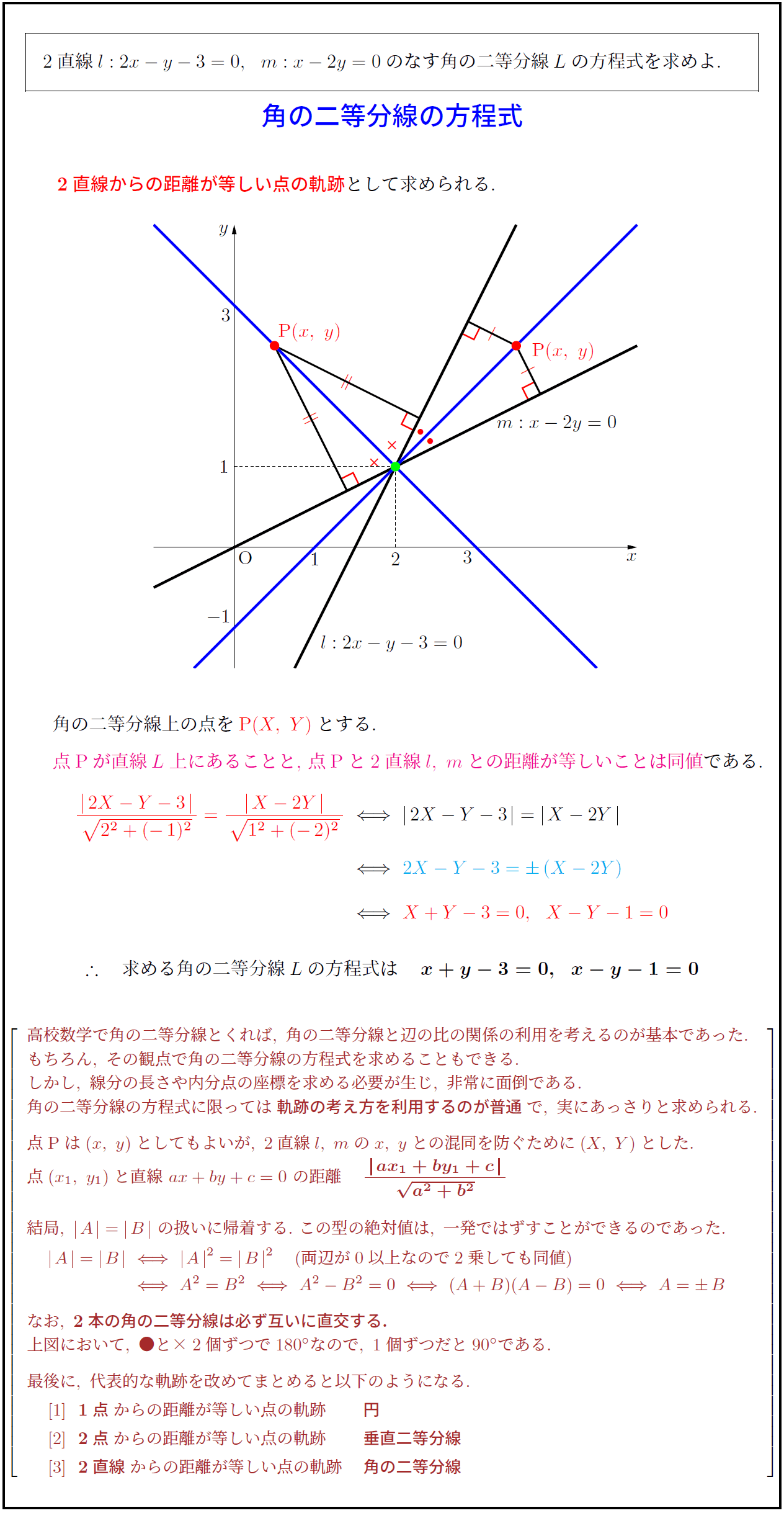
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも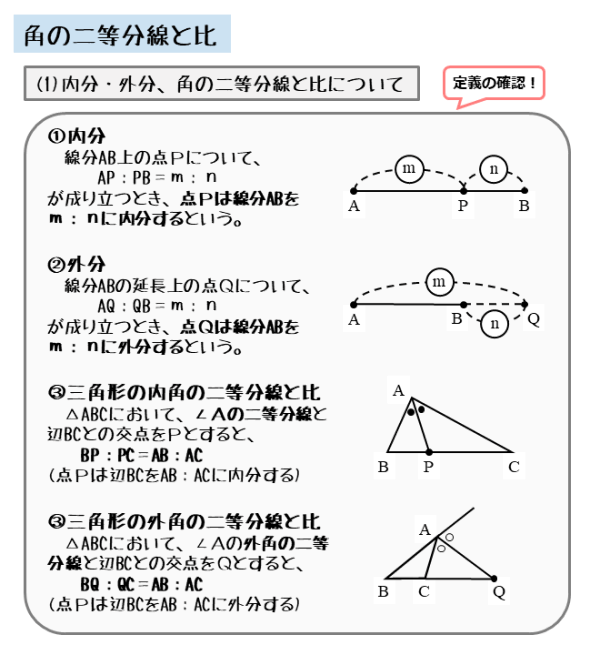
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも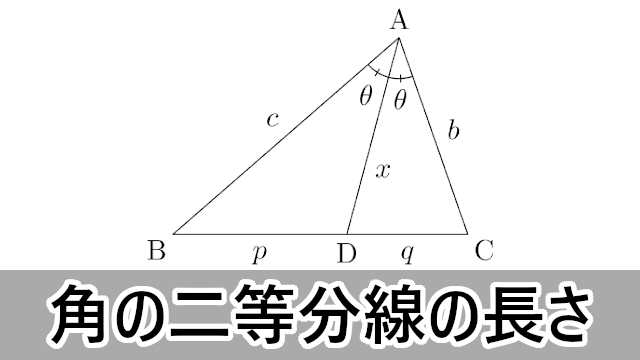
二等分線と垂線の定理 Fukusukeの数学めも	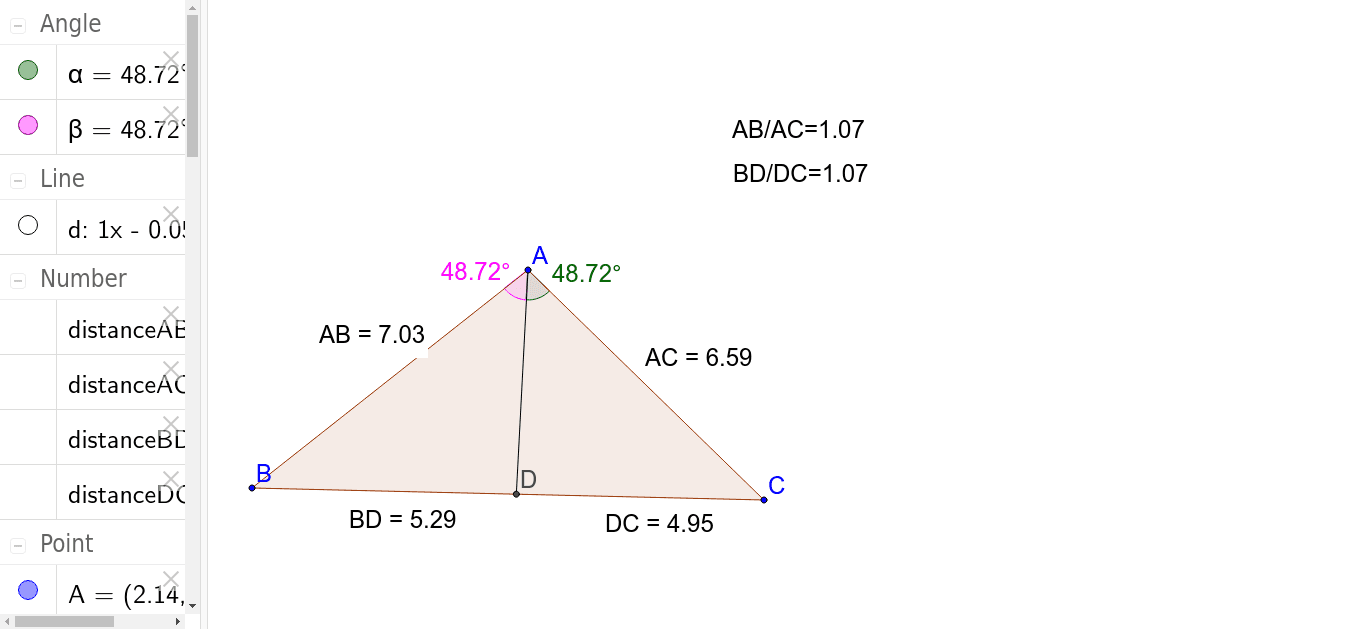二等分線と垂線の定理 Fukusukeの数学めも	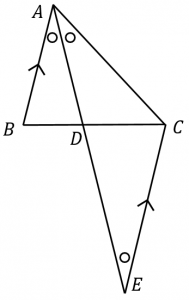二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	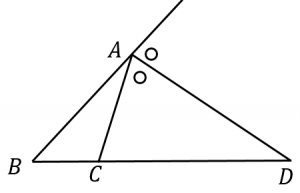二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	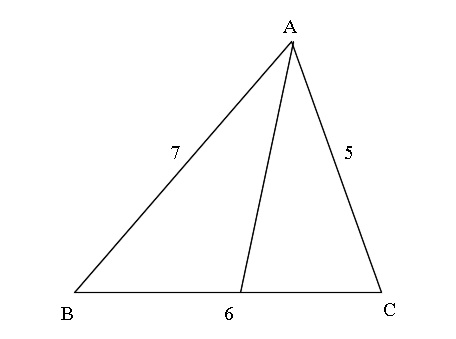二等分線と垂線の定理 Fukusukeの数学めも	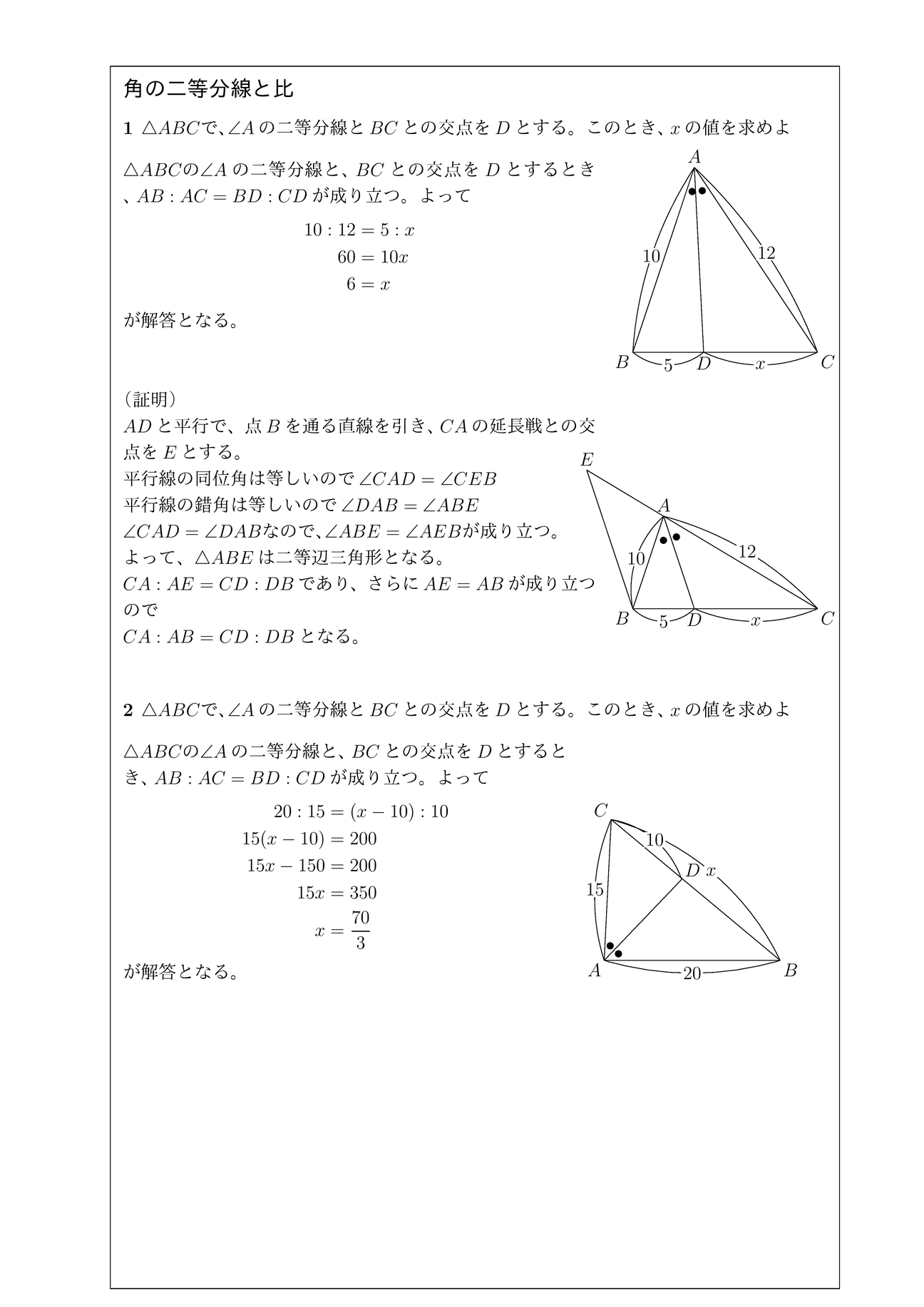二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	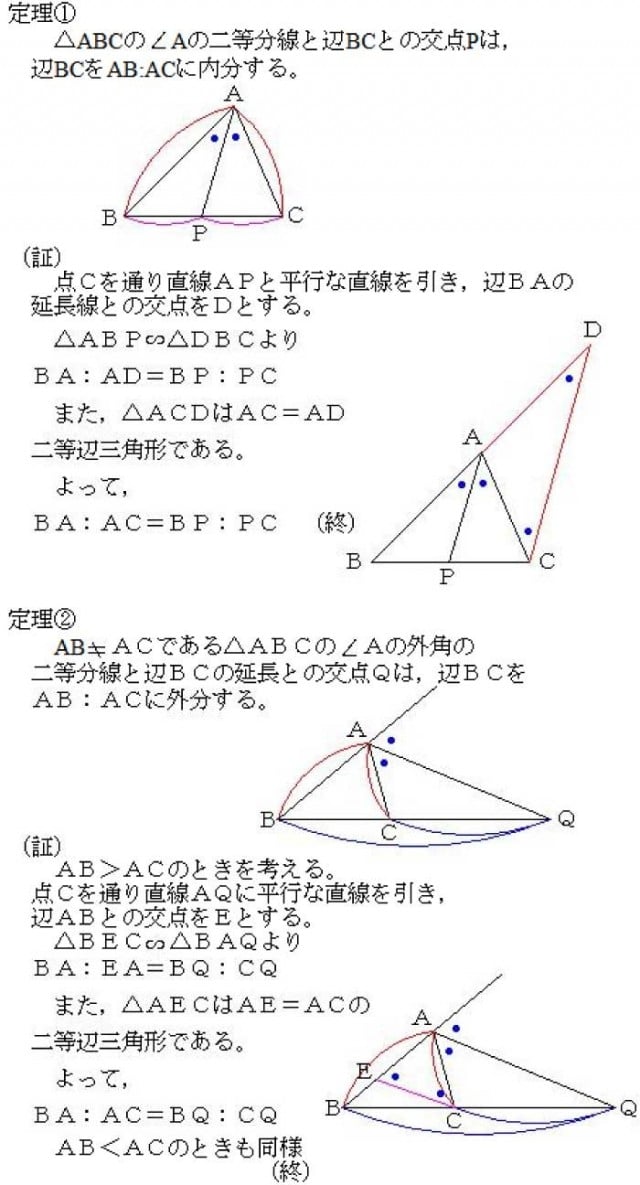二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも
二等分線と垂線の定理 Fukusukeの数学めも	二等分線と垂線の定理 Fukusukeの数学めも

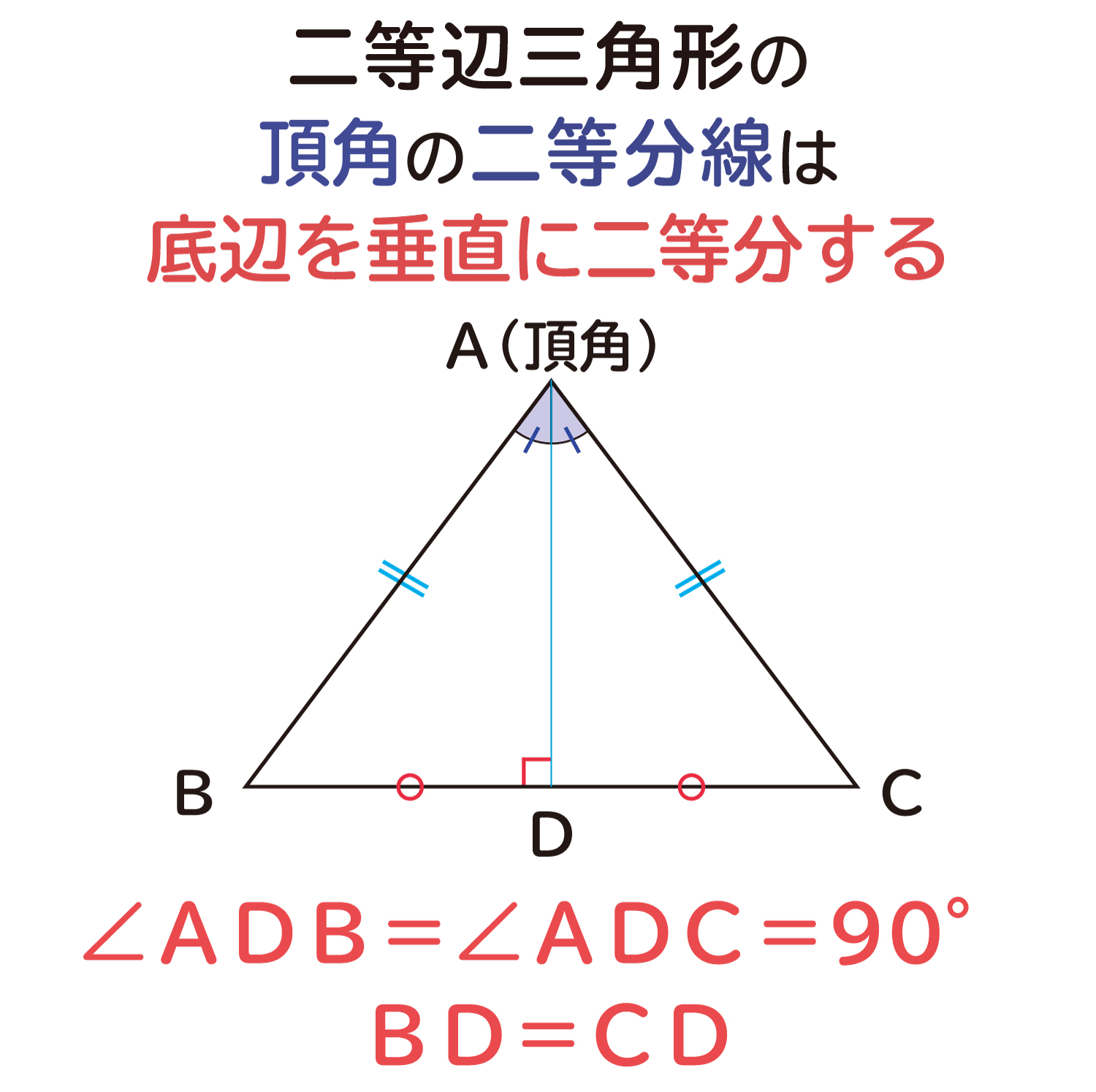
8 二等辺三角形の性質 ①両底角が等しい ②頂点の二等分線と底角の垂直二等 分線は一致する 9 平行四辺形の性質 ①2組の向かい合う辺はそれぞれ等しい ②1組の向かい合う辺が平行で等しい ③2組の向かい合う角はそれぞれ等しい ④対角線は互いに他を2 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか まとめ：直角三角形の比3つを

Incoming Term: 三角形の角の二等分線と比 証明, 三角形の角の二等分線と比,